4. Wertschöpfung, Gewinn, Rentabilität, Deckungsbeitrag
4.5 Deckungsbeitrag (DB) [BWL 4520]
Kapitelstart Vorherige Seite Nächste Seite Kapitel 1 Kapitel 2 Kapitel 3 Kapitel 5 Kapitel 64.5 Deckungsbeitrag
4.5.2 Gewinnschwellenanalyse
a) Aufgabenstellung, Begriffsbestimmung
Als ein weiteres wichtiges Anwendungsfeld der Teilkostenrechnung und der darauf beruhenden Deckungsbeitragsrechnung ist die sog. Gewinnschwellenanalyse (Break-even-Analyse) zu nennen.
 |
Aufgabe und Anliegen der Gewinnschwellenanalyse ist es, jene Umsatzgröße U0 [EUR] bzw. jene Produktions- bzw. Absatzmenge x0 [ME] zu ermitteln, bei der die Umsatzerlöse E0 [EUR] (mit E0 = U0) die Kosten K0 [EUR], bestehend aus den Fixkosten Kf und den entsprechenden variablen Kosten Kv, genau decken, so dass sich für den Gewinn G [EUR] der Wert G = E0 - K0 = 0 ergibt. Diese Größe ist der sog. Break-even-Point. |
Eine solche Gewinnschwellenanalyse kann sowohl umsatzbezogen als auch produkt- bzw. auftragsbezogen durchgeführt werden..
b) Umsatzbezogene Gewinnschwelle: Rechnerische Lösung
Die gesuchte Größe U0 (= E0) kann rechnerisch und auch grafisch ermittelt werden. Betrachten wir zunächst die rechnerische Lösung des Problems:
Aus dem Ansatz, dass am Break-even-Point die umsatzbezogenen Erlöse E0 genau den Gesamtkosten K0 entsprechen, folgt zunächst:
E0 = K0 = Kf + Kv = U0. (1)
Aufgrund einer naheliegenden Annahme, dass sich die variablen Kosten in einem größeren Wertebereich proportional zum Umsatz U verhalten, benötigen wir die Angabe, wie hoch im Durchschnitt der Anteil der variablen Kosten Kv am Umsatz U ist.
Wird dieser Anteil - wie bereits an anderer Stelle ausgeführt - mit einer Größe a [%] bezeichnet, kann die obige Gleichung (1) auch wie folgt geschrieben werden:
E0 = Kf + a * U0 / 100 = U0. (2)
Die Gleichung (2) gilt es nach der gesuchten Größe U0 umzustellen. Zu diesem Zweck sind beide Seiten zunächst mit 100 zu multiplizieren. Wir erhalten:
Kf * 100 + a * U0 = U0 * 100. (3)
Wird diese Gleichung nach der Größe U0 umgestellt, erhalten wir folgende Bestimmungsgleichung für die Ermittlung der umsatzbezogenen Gewinnschwelle:
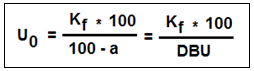
Es bedeuten:
U0 Break-even-Umsatz [EUR],
Kf Fixkosten [EUR]
a Anteil der variablen Kosten am Umsatz [%]
DBU prozentualer Deckungsbeitrag des Umsatzes [%], mit DBU = 100 [%] - a [%].
Zur Beachtung:
Aus G = U0 – Kv,0 – Kf = 0 bzw. aus G = DB0 – Kf = 0 folgt DB0 = Kf, das heißt, am Break-even-Point entspricht der Deckungsbeitrag DB0 genau der Höhe der Fixkosten Kf.
Die Formel für die Ermittlung der umsatzbezogenen Gewinnschwelle ist für den Fall, dass nicht ein Gewinn von G = 0, sondern ein Ziel-Gewinn G mit G > 0 erreicht werden soll, wie folgt zu erweitern:
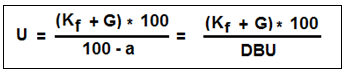 .
.
In den Wissenstests zu diesem Lern-Modul können hierzu Fallbeispiele durchgerechnet werden.
