4. Wertschöpfung, Gewinn, Rentabilität, Deckungsbeitrag
4.5 Deckungsbeitrag (DB) [BWL 4521]
Kapitelstart Vorherige Seite Nächste Seite Kapitel 1 Kapitel 2 Kapitel 3 Kapitel 5 Kapitel 64.5 Deckungsbeitrag
4.5.2 Gewinnschwellenanalyse
c) Umsatzbezogene Gewinnschwelle: Grafische Lösung
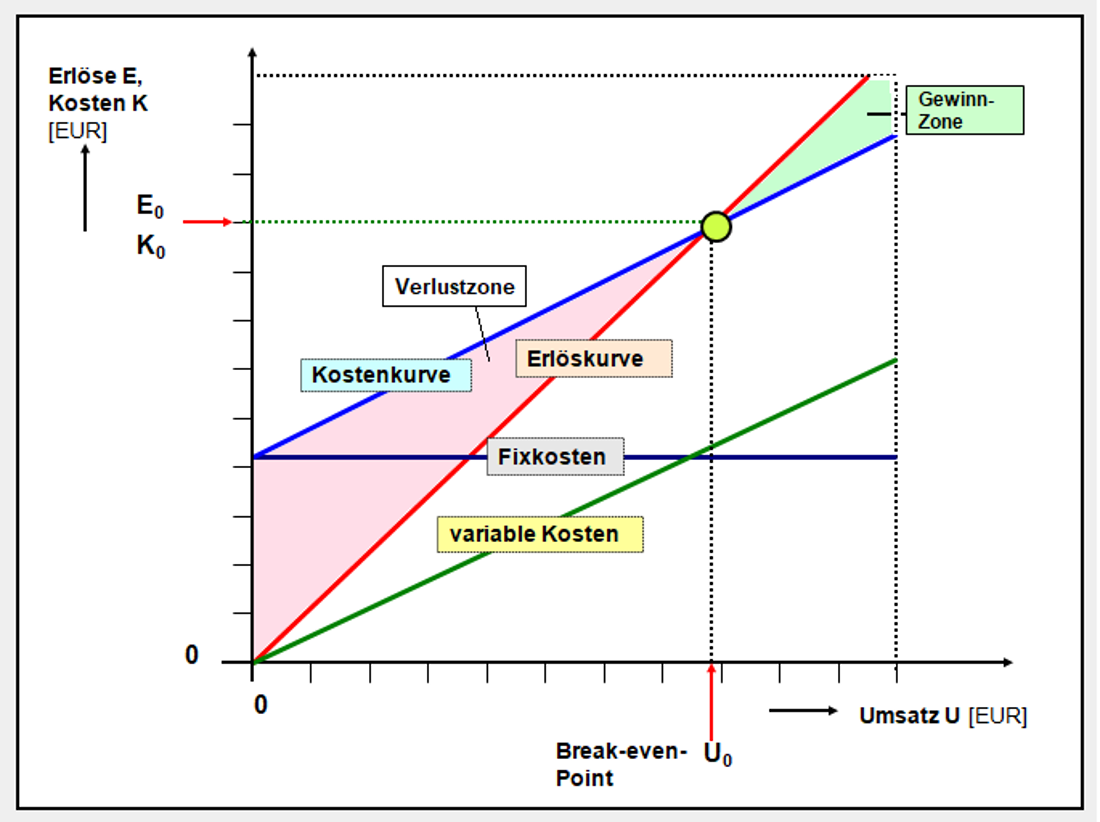
Für die grafischen Lösung des skizzierten Problems wird ein x,y-Diagramm benötigt, wobei auf der x-Achse der Umsatz U [EUR] und auf der y-Achse die Umsatzerlöse E [EUR] sowie die Kosten K [EUR] abgetragen werden.
Wenn davon ausgegangen werden kann, dass die Umsätze U ohne Erlösschmälerungen zu Erlösen E transferiert werden, kann die sogenannte Erlöskurve E = f (U) als Gerade mit einem Abstieg von 45o ins das Diagramm eingetragen werden.
Die Fixkostenkurve Kf = f (U) ist eine Parallele zur x-Achse, während die Kurve der variablen Kosten Kv = f (U) als eine Gerade mit dem Anstieg von a/100 * U in das Diagramm einzutragen ist.
Die Gesamtkostenkurve K = f (U) beginnt bei U = 0 auf der y-Achse beim Wert der Fixkosten Kf und verläuft dann im Weiteren parallel zur Kurve der variablen Kosten.
Der Break-even-Point ist jener Punkt im x, y - Diagramm, bei dem die Gesamtkostenkurve K = f (U) die Erlöskurve E = f (U) schneidet, denn hier gilt Erlöse E = Kosten K = Umsatz U.
Die Gewinnschwellenwerte sind auf der x-Achse dort abzulesen, wo ein Lot vom Break-even-Point die x-Achse schneidet (siehe Abb. 4.18).