4. Wertschöpfung, Gewinn, Rentabilität, Deckungsbeitrag
4.5 Deckungsbeitrag (DB) [BWL 4522]
Kapitelstart Vorherige Seite Nächste Seite Kapitel 1 Kapitel 2 Kapitel 3 Kapitel 5 Kapitel 64.5 Deckungsbeitrag
4.5.2 Gewinnschwellenanalyse
d) Produktbezogene Gewinnschwelle
| Für die rechnerische Bestimmung der produkt- bzw. auftragsbezogenen Gewinnschwelle können folgende Ansätze genutzt werden: Der Break-even-Point ist auch in diesem Falle jener Punkt, an dem die Erlöse E0 genau den Gesamtkosten K0 entsprechen: E0 = K0 = Kf + Kv. (1) Für die Erlöse E und die Kosten K gelten wiederum die folgenden Bestimmungsgleichungen: E [EUR] = P [EUR/ME] * x [ME], (2) K [EUR] = Kf [EUR] + kv [EUR/ME] * x [ME]. (3) Da bei der Gewinnschwelle nach Gleichung (1) die Beziehung E0 = K0 gilt, folgt mit Bezugnahme auf die Gleichungen (2) und (3): P * x0 = Kf + kv * x0 . (4). Wird diese Gleichung nach der gesuchten Größe x0 umgestellt, erhalten wir folgende Bestimmungsgleichung für die Ermittlung der produkt- bzw. auftragsbezogenen Gewinnschwelle: 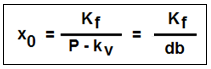 Es bedeuten: x0 Break-even-Menge [ME], Kf Fixkosten des Unternehmens [EUR], P Verkaufspreis [EUR/ME], kv variable Stückkosten [EUR/ME], db Stück-Deckungsbeitrag [EUR/ME] ("kleiner" DB) mit db = P ./. kv. Die Formel für die Ermittlung der produktbezogenen Gewinnschwelle ist für den Fall, dass nicht ein Gewinn von G = 0, sondern ein Ziel-Gewinn G mit G > 0 erreicht werden soll, wie folgt zu erweitern: 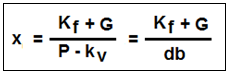 |
| Für die graphische Lösung von Aufgaben einer produkt- bzw. auftragsbezogenen Gewinnschwellenanalyse ist wiederum ein x,y-Diagramm zu wählen, wobei auf der x-Achse diesmal die zu ermittelnde Absatzmenge (Symbol x [ME]) und auf der y-Achse wie bisher die Umsatzerlöse E [EUR] sowie die Fixkosten Kf [EUR], die variablen Kosten Kv [EUR] sowie die Gesamtkosten K [EUR] abgetragen werden. Der Gewinnschwellenwert (Absatzmenge x0 [ME]) ist auf der x-Achse dort abzulesen, wo ein Lot vom Break-even-Point die x-Achse schneidet. Die mit dieser Absatzmenge verbundenen Erlöse E0 und Kosten K0 sind auf der y-Achse dort abzulesen, wo eine in Höhe des Break-even-Points gezogene Gerade die y-Achse scheidet (siehe die Beispiel-Darstellung in Abb. 4.19). |